Introducción
Como muchas disciplinas, la termodinámica surge de los procedimientos empíricos que llevaron a la construcción de elementos que terminaron siendo muy útiles para el desarrollo de la vida del hombre.
Creemos que la termodinámica es un caso muy especial debido a que sus inicios se pierden en la noche de los tiempos mientras que en la actualidad los estudios sobre el perfeccionamiento de las máquinas térmicas siguen siendo de especial importancia, mas aun si tomamos en cuenta la importancia que revisten temas de tanta actualidad como la contaminación.
El origen fué sin lugar a dudas la curiosidad que despertara el movimiento producido por la energía del vapor de agua.
Su desarrollo fué tomando como objetivo principal el perfeccionamiento de las tecnologias aplicadas con el fin de hacer mas facil la vida del hombre, reemplazando el trabajo manual por la máquina que facilitaba su realización y lograba mayor rapidez, estos avances que gravitaban directamente en la economía, por ello el inicio se encuentra en el bombeo de aguas del interior de las minas y el transporte.
Mas tarde se intensificaron los esfuerzos por lograr el máximo de rendimiento lo que llevó a la necesidad de lograr un conocimiento profundo y acabado de las leyes y principios que regian las operaciones realizadas con el vapor.
El campo de la termodinámica y su fuente primitiva de recursos se amplía en la medida en que se incorporan nuevas áreas como las referentes a los motores de combustión interna y ultimamente los cohetes. La construcción de grandes calderas para producir enormes cantidades de trabajo marca tambien la actualidad de la importancia del binomio máquinas térmicas-termodinámica.
En resumen: en el comienzo se partió del uso de las propiedades del vapor para succionar agua de las minas, con rendimientos insignificantes, hoy se trata de lograr las máximas potencias con un mínimo de contaminación y un máximo de economía.
Para realizar una somera descripción del avance de la termodinámica a través de los tiempos la comenzamos identificando con las primitivas máquinas térmicas y dividimos su descripción en tres etapas, primero la que dimos en llamar empírica, la seguna la tecnológica y la tercera la científica.
I.- La etapa empírica
Los orígenes de la termodinámica nacen de la pura experiencia y de hallazgos casuales que fueron perfeccionándose con el paso del tiempo.
Algunas de las máquinas térmicas que se construyeron en la antigüedad fueron tomadas como mera curiosidad de laboratorio, otros se diseñaron con el fin de trabajar en propósitos eminentemente prácticos. En tiempos del del nacimiento de Cristo existian algunos modelos de máquinas térmicas, entendidas en esa época como instrumentos para la creación de movimientos autónomos, sin la participación de la tracción a sangre.
El ingenio más conocidos por las crónicas de la época es la eolipila de Herón que usaba la reacción producida por el vapor al salir por un orificio para lograr un movimiento. Esta máquina es la primera aplicacióndel principio que usan actualmente las llamadas turbinas de reacción.
La historia cuenta que en 1629 Giovanni Branca diseñó una máquina capaz de realizar un movimiento en base al impulso que producía sobre una rueda el vapor que salía por un caño. No se sabe a ciencia cierta si la máquina de Branca se construyó, pero, es claro que es el primer intento de construcción de las que hoy se llaman turbinas de acción.
La mayor aplicación de las posibilidades de la máquina como reemplazante de la tracción a sangre consistía en la elevación de agua desde el fondo de las minas. Por ello la primera aplicación del trabajo mediante la fuerza del vapor cristaliza en la llamada máquina de fuego de Savery.
La máquina de Savery consistía en un cilindro conectado mediante una cañería a la fuente de agua que se deseaba bombear, el cilindro se llenaba de vapor de agua, se cerraba la llave de ingreso y luego se enfriaba, cuando el vapor se condensaba se producía un vacío que permitía el ascenso del agua.
II.- La etapa tecnológica.
Según lo dicho la bomba de Savery no contenía elementos móviles, excepto las válvulas de accionamiento manual, funcionaba haciendo el vacío, de la misma manera en que ahora lo hacen las bombas aspirantes, por ello la altura de elevación del agua era muy poca ya que con un vacío perfecto se llegaría a lograr una columna de agua de 10.33 metros, pero, la tecnología de esa época no era adecuada para el logro de vacios elevados.
El primer aparato elemento que podriamos considerar como una máquina propiamente dicha, por poseer partes móviles, es la conocida como máquina de vapor de Thomas Newcomen construída en 1712. La innovación consistió en la utilización del vacío del cilindro para mover un pistón que a su vez proveía movimiento a un brazo de palanca que actuaba sobre una bomba convencional de las llamadas aspirante-impelente.
Podemos afirmar que es la primera máquna alternativa de mla que se tiene conocimiento y que con ella comienza la historia de las máquinas térmicas.
Las dimensiones del cilindro, órgano principal para la creación del movimien-to, eran: 53,3 cm de diámetro y 2,4 metros de altura, producía 12 carreras por minuto y elevaba 189 litros de agua desde una profundidad de 47,5 metros.
El principal progreso que se incorpora con la máquina de Newcomen consis-te en que la producción de un movimiento oscilatorio habilita el uso de la máquina para otros servicios que requieran movimiento alternativo, es decir, de vaivén.
En esa época no existian métodos que permitieran medir la potencia desarrollada por las máquinas ni unidades que permitieran la comparación de su rendi-miento, no obstante, los datos siguientes dan una idea del trabajo realizado por una máquina que funcionó en una mina en Francia, contaba con un cilindro de 76 cm de diámetro y 2,7 metros de altura, con ella se pudo completar en 48 horas una labor de desagote que previamente había requerido una semana con el traba-jo de 50 hombres y 20 caballos operando en turnos durante las 24 horas del día.
La máquina de Newcomen fué perfeccionada por un ingeniero inglés llamado Johon Smeaton (1742-1792). Un detalle de la potencia lograda lo podemos ver en el trabajo encargado por Catalina II de Rusia quien solicitó bombear agua a los di-ques secos del fuerte de Kronstadt. Esta tarea demoraba un año usando molinos de viento de 100 metros de altura, la máquina de Smeaton demoró solamente dos semanas. Se debe destacar que el perfeccionamiento consistió en la optimización de los mecanismos, cierres de válvulas, etc.
El análisis de las magnitudes que entran en juego en el funcionamiento de la máquina de vapor y su cuantificación fué introducido por James Watt (1736-1819). Watt se propuso estudiar la magnitud del calor puesto en juego en el funcio-namiento de la máquina, esto permitiría estudiar su rendimiento.
El mayor obstáculo que encontró Watt fué el desconocimiento de los valores de las constantes físicas involucradas en el proceso, a raiz de ello debió realizar un proceso de mediciones para contar con datos confiables. Sus mediciones experimentales le permitieron verificar que la máquina de Newcomen solo usaba un 33% del vapor consumido para realizar el trabajo útil.
Los aportes de Watt son muchos, todos ellos apuntaron al logro de un mayor rendimiento, inventó el prensaestopa que actua manteniendo la presión mientras se mueve el bástago del pistón, introdujo la bomba de vacío para incrementar el rendimiento en el escape, ensayó un mecanismo que convirtiera el movimiento alternativo en rotacional, en 1782 patentó la máquina de doble efecto (el vapor empuja en ambas carreras del pistón), ideó válvulas de movimiento vertical que permitian mantener la presión de la caldera mediante la fuerza de un resorte com-primido. Creó el manómetro para medir la presión del vapor y un indicador que po-día dibujar la evolución presión-volumen del vapor en el cilindro a lo largo de un ciclo. Con el objetivo de establecer una unidad adecuada para la medición de la potencia, realizó experiencias para definir el llamado caballo de fuerza. Determinó que un caballo podía desarrollar una potencia equivalente a levantar 76 kg hasta una altura de 1 metro en un segundo, siguiendo con este ritmo durante cierto tiempo, este valor se usa actualmente y se lo llama caballo de fuerza inglés.
Un detalle importante de las calderas de Watt es que trabajaban a muy baja presión, 0,3 a 0,4 kg/cm2.
Los progresos tecnológicos aportados por Watt llevaron la tecnología de la máquina de vapor a un refinamiento considerable. Se había avanzado en seguri-dad merced a la incorporación de válvulas, ya se contaba con unidades que daban cuenta de la potencia y el rendimiento, los mecanismos fueron elaborados con los mas recientes avances de la tecnología mecánica. Lo único que no entró en la consideración de Watt fué la posibilidad de usar calderas de mayor presión, su objetivo principal era la seguridad, y desde el punto de vista económico no reque-ría perfeccionamiento, sus máquinas eran muy apreciadas y se vendian bien.
Después de Watt se consiguieron considerables avances en la utilización de calderas de muy alta presión, esta incorporación incrementó el rendimiento y, lo mas importante, favoreció el uso de calderas de menor tamaño que realizaban mayor trabajo que las grandes, además de mejorar el rendimiento del vapor las preparó para adaptarlas para su instalación en medios de transporte.
En agosto de 1807 Robert Fulton puso en funcionamiento el primer barco de vapor de éxito comercial, el Clermont, el mérito de Fulton consiste en la instalación y puesta en marcha de una máquina de vapor a bordo, no realizó innovaciones sobre la máquina en sí. Este barco cumplió un servicio fluvial navegando en el río Hudson.
En el año 1819 el buque de vapor Savannah, de bandera norteamericana realiza el primer viaje transatlántico, ayudado por un velamen. El Britania fué el primer barco de vapor inglés, entró en servicio en 1840, desplazaba 1150 toneladas y contaba con una máquina de 740 caballos de fuerza, alimentada por cuatro calderas de 0.6 kg/cm cuadrado, desarrollando una velocidad de 14 km/h.
George Stephenson (1781-1848) fué el primero que logró instalar una máquina de vapor sobre un vehículo terrestre dando inicio a la era del ferrocarril.
En el año 1814 Stephenson logró arrastrar una carga de treinta toneladas por una pendiente de 1 en 450 a sis km por hora.
En 1829 la locomotora llamada Rocket recorrió 19 km en 53 minutos lo que fué un record para la época.
III.- Etapa científica.
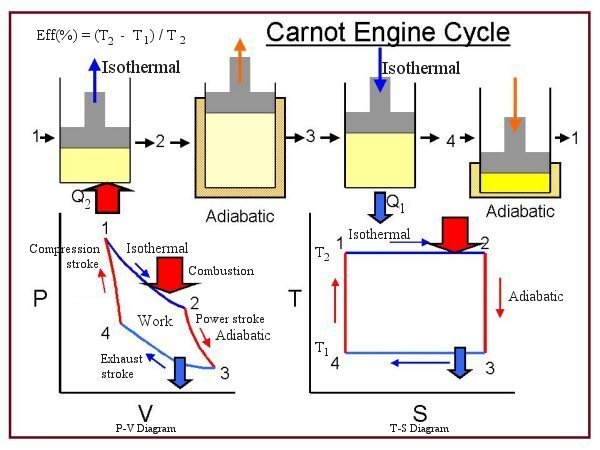
Sadi Carnot (1796-1832) es el fundador de la termodinámica como disciplina teórica, escribió su trabajo cumbre a los 23 años. Este escrito estuvo desconocido durante 25 años hasta que el físico Lord Kelvin redescubriera la importancia de las propuestas contenidas en él.
Llamó la atención de Carnot el hecho de que no existieran teorias que ava-laran la propuestas utilizadas en el diseño de las máquinas de vapor y que todo ello dependira de procedimientos enteramente empíricos. Para resolver la cuestión propuso que se estudiara todo el procedimiento desde el punto de vista mas gene-ral, sin hacer referencia a un motor, máquina o fluido en especial.
Las bases de las propuestas de Carnot se pueden resumir haciendo notar que fué quien desarrolló el concepto de proceso cíclico y que el trabajo se produ-cía enteramente "dejando caer" calor desde una fuente de alta temperatura hasta un depósito a baja temperatura. También introdujo el concepto de máquina reversible.
El principio de Carnot establece que la máxima cantidad de trabajo que puede ser producido por una máquina térmica que trabaja entre una fuente a alta temperatura y un depósito a temperatura menor, es el trabajo producido por una máquina reversible que opere entre esas dos temperaturas. Por ello demostró que ninguna máquina podía ser mas eficiente que una máquina reversible.
A pesar que estas ideas fueron expresadas tomando como base la teoría del calórico, resultaron válidas. Posteriormente Clausius y Kelvin, fundadores de la termodinámica teórica, ubicaron el principio de Carnot dentro de una rigurosa teo-ría científica estableciendo un nuevo concepto, el segundo principio de la termodinámica.
Carnot también establece que el rendimiento de cualquier máquina térmica depende de la diferencia entre temperatura de la fuente mas caliente y la fría. Las altas temperaturas del vapor presuponen muy altas presiones y la expansión del vapor a bajas temperaturas producen grandes volúmenes de expansión. Esto producía una cota en el rendimiento y la posibilidad de construcción de máquinas de vapor.
En esta época todavía tenía vigencia la teoría del calórico, no obstante ya estaba germinando la idea de que esa hipótesis no era la adecuada, en el marco de las sociedades científicas las discusiones eran acaloradas. James Prescot Joule (1818-1889) se convenció rapidamente de que el trabajo y el calor eran diferentes manifestaciones de una misma cosa. Su expe-riencia mas recordada es aquella en que logra medir la equivalencia entre el traba-jo mecánico y la cantidad de calor. Joule se valió para esta experiencia de un sis-tema de hélices que agitaban el agua por un movimiento producido por una serie de contrapesos que permitian medir la energía mecánica puesta en juego.
A partir de las investigaciones de Joule se comenzó a debilitar la teoría del calórico, en especial en base a los trabajos de Lord Kelvin quien junto a Clausius terminaron de establecer las bases teóricas de la termodinámica como disciplina independiente. En el año 1850 Clausius dscubrió la existencia de la entropía y enunció el segundo principio:
Es imposible que una máquina térmica que actúa por sí sola sin recibir ayuda de ningún agente externo, transporte calor de un cuerpo a otro que está a mayor temperatura.
En 1851 Lord Kelvin publicó un trabajo en el que compatibilizaba los estudios de Carnot, basados en el calórico, con las conclusiones de Joule, el calor es una forma de energía, compartió las investigaciones de Clausius y reclamó para sí el postulado del primer principio que enunciaba así:
Es imposible obtener, por medio de agentes materiales inanimados, efectos mecánicos de cualquier porción de materia enfriándola a una temperatura inferior a la de los objetos que la rodean. Lord Kelvin también estableció un principio que actualmente se conoce como el primer principio de la termodinámica. Y junto a Clausius derrotaron la teoría del calórico.
Situación Actual
Hoy se ha llegado a uninteresante perfeccionamiento de las máquinas térmicas, sobre una teoría basada en las investigaciones de Clausius, Kelvin y Carnot, cuyos principios están todavía en vigencia, la variedad de máquinas térmicas va desde las grandes calderas de las centrales nucleares hasta los motores cohete que impulsan los satélites artificiales, pasando por el motor de explosión, las turbinas de gas, las turbinas de vapor y los motores de retropropulsión. Por otra parte la termodinámica como ciencia actua dentro de otras disciplinas como la química, la biología, etc.
Conclusión
El desarrollo de la termodinámica tiene un origen empírico como muchas de las partes de la tecnología.
Una de las curiosidades en la aplicación temprana de efectos del vapor en la etapa que dimos en llamar empírica y que a lo largo de su desarrollo cambiara su origen en varias hipótesis, flogisto, calórico y finalmente energía.
Con Watt se logra el perfeccionamiento en la tecnología, se comprenden los principios básicos de la misma y se aislan las variables que intervienen en el fun-cionamiento de la máquina, la introducción de la unidad para medir la potencia conduce al manejo de criterios de comparación.
Despues de Watt comienza el desarrollo de las máquinas móviles con las realizaciones de Robert Fulton y George Stephenson.
Tambien es importante marcar como las teorias de Carnot tienen aún validez en su forma original apesar de haber estado fundamentadas en una hipótesis erro-nea, la del calórico. Carnot introduce tres conceptos fundamentales:
El concepto de ciclo o máquina cíclica.
La relación entre la "caida del calor de una fuente caliente a otra mas fría y su relación con el trabajo.
El concepto de máquina reversible de rendimiento máximo.
Gracias a Clausius y Kelvin se convierte a la termodinámica en una ciencia independiente de alto contenido teórico y matemático, lo que logra entender los fenómenos que se desarrollaban y fundamentar progresos tecnológicos.
Bibliografía de referencia
| Motores térmicos e hidráulicos | Rosich | Ergon |
| Termodinámica Técnica | Estrada | Editorial Alsina. |
| Maquinas Térmicas | Sandfort | Eudeba |
| A TextBook on Heat | Barton | Longsman |
| Heat | Mitton | Dent and sons |
Las palabras clave se refieren a los precursores de esta ciencia: Herón, Savery, Newcomen, Fulton, Stephenson, Sadi Carnot, Clausius, Lord Kelvin, Joule, Watt.
Bárbara Scarlett Betancourt Morales
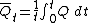
 dN ---------- (2)
dN ---------- (2) ) is defined as mass per unit volume.
) is defined as mass per unit volume.


 T = T2 - T1, thus the system's total energy E is constant (via the first law of thermodynamics), while its free energy F decreases, and its entropy S rises (via the second law of thermodynamics), until finally
T = T2 - T1, thus the system's total energy E is constant (via the first law of thermodynamics), while its free energy F decreases, and its entropy S rises (via the second law of thermodynamics), until finally  0 at equilibrium.
0 at equilibrium.